The
special theory of relativity was proposed in
1905 by
Albert Einstein in his article "
On the Electrodynamics of Moving Bodies". Some three centuries earlier,
Galileo's principle of relativity had stated that all
uniform motion was relative, and that there was no absolute and well-defined state of rest; a person on the deck of a ship may be at rest in his opinion, but someone observing from the shore would say that he was moving. Einstein's theory generalized
Galilean relativity from only mechanics to all laws of physics including
electrodynamics. To stress this point, Einstein not only widened the postulate of relativity, but added the second postulate - that all observers will always measure the
speed of light to be the same no matter what their state of uniform linear motion is.
This theory has a variety of surprising consequences that seem to violate common sense, but all have been
experimentally verified. Special relativity overthrows
Newtonian notions of absolute space and time by stating that distance and
time depend on the observer, and that time and space are perceived differently, depending on the observer. It yields the equivalence of
matter and
energy, as expressed in the
mass-energy equivalence formula
E =
mc², where
c is the speed of light in a vacuum. Special relativity agrees with Newtonian mechanics in their common realm of applicability, in experiments in which all velocities are small compared to the speed of light.
The theory was called "special" because it applies the
principle of relativity only to
inertial frames. Einstein developed
general relativity to apply the principle generally, that is, to any frame, and that theory includes the effects of
gravity. Special relativity does not account for gravity, but it can deal with accelerations.
Although special relativity makes some quantities relative, such as time, that we would have imagined to be absolute based on everyday experience, it also makes absolute some others that we would have thought were relative. In particular, it states that the speed of light is the same for all observers, even if they are in motion relative to one another. Special relativity reveals that
c is not just the velocity of a certain phenomenon - light - but rather a fundamental feature of the way space and time are tied together. In particular, special relativity states that it is impossible for any material object to accelerate to light speed.
For history and motivation, see the article: history of special relativity Postulates The
principle of relativity, which states that there is no stationary reference frame, dates back to
Galileo, and was incorporated into Newtonian Physics. However, in the late 19 century, the existence of
electromagnetic waves led some physicists to suggest that the universe was filled with a substance known as "
aether", which would act as the medium through which these waves, or vibrations traveled. The aether was thought to constitute an absolute reference frame against which speeds could be measured. In other words, the aether was the only fixed or motionless thing in the universe. Aether supposedly had some wonderful properties: it was sufficiently elastic that it could support electromagnetic waves, and those waves could interact with matter, yet it offered no resistance to bodies passing through it. The results of various experiments, including the
Michelson-Morley experiment, indicated that the Earth was always 'stationary' relative to the aether — something that was difficult to explain, since the Earth is in orbit around the Sun. Einstein's elegant solution was to discard the notion of an aether and an absolute state of rest. Special relativity is formulated so as to not assume that any particular frame of reference is special; rather, in relativity, any reference frame moving with uniform motion will observe the same laws of physics. In particular, the speed of light in a vacuum is always measured to be
c, even when measured by multiple systems that are moving at different (but constant) velocities.
Lack of an absolute reference frame Main article: Consequences of special relativity Einstein has said that all of the consequences of special relativity can be derived from examination of the
Lorentz transformations.
These transformations, and hence special relativity, lead to different physical predictions than Newtonian mechanics when relative velocities become comparable to the speed of light. The speed of light is so much larger than anything humans encounter that some of the effects predicted by relativity are initially counter-intuitive:
Time dilation — the time lapse between two events is not invariant from one observer to another, but is dependent on the relative speeds of the observers' reference frames (e.g., the
twin paradox which concerns a twin who flies off in a spaceship traveling near the speed of light and returns to discover that his twin has aged much more).
Relativity of simultaneity — two events happening in two different locations that occur simultaneously to one observer, may occur at different times to another observer (lack of
absolute simultaneity).
Lorentz contraction — the dimensions (e.g., length) of an object as measured by one observer may be smaller than the results of measurements of the same object made by another observer (e.g., the
ladder paradox involves a long ladder traveling near the speed of light and being contained within a smaller garage).
Composition of velocities — velocities (and speeds) do not simply 'add', for example if a rocket is moving at ⅔ the speed of light relative to an observer, and the rocket fires a missile at ⅔ of the speed of light relative to the rocket, the missile does not exceed the speed of light relative to the observer. (In this example, the observer would see the missile travel with a speed of 12/13 the speed of light.)
Inertia and momentum — as an object's velocity approaches the speed of light from an observer's point of view, its mass appears to increase thereby making it more and more difficult to accelerate it from within the observer's frame of reference.
Equivalence of mass and energy, E = mc² — The energy content of an object at rest with mass m equals
mc. Conservation of energy implies that in any reaction a decrease of the sum of the masses of particles must be accompanied by an increase in kinetic energies of the particles after the reaction. Similarly, the mass of an object can be increased by taking in kinetic energies.
Consequences Full article: Lorentz transformations Relativity theory depends on "
reference frames". A reference frame is an observational perspective in space at rest, or in uniform motion, from which a position can be measured along 3 spatial axes. In addition, a reference frame has the ability to determine measurements of the time of events using a 'clock' (any reference device with uniform periodicity).
An event is an occurrence that can be assigned a single unique time and location in space relative to a reference frame: it is a "point" in
space-time. Since the speed of light is constant in relativity in each and every reference frame, pulses of light can be used to unambiguously measure distances and refer back the times that events occurred to the clock, even though light takes time to reach the clock after the event has transpired.
For example, the explosion of a firecracker may be considered to be an "event". We can completely specify an event by its four space-time coordinates: The time of occurrence and its 3-dimensional spatial location define a reference point. Let's call this reference frame S.
In relativity theory we often want to calculate the position of a point from a different reference point.
Suppose we have a second reference frame S', whose spatial axes and clock exactly coincide with that of S at time zero, but it is moving at a constant velocity

with respect to S along the

-axis.
Since there is no absolute reference frame in relativity theory, a concept of 'moving' doesn't strictly exist, as everything is always moving with respect to some other reference frame. Instead, any two frames that move at the same speed in the same direction are said to be
comoving. Therefore S and S' are not
comoving.
Let's define the
event to have space-time coordinates

in system S and
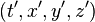
in S'. Then the Lorentz transformation specifies that these coordinates are related in the following way:
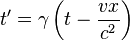

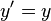

where
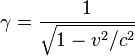
is called the
Lorentz factor and

is the
speed of light in a vacuum.
The

and
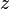
coordinates are unaffected, but the

and
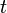
axes are mixed up by the transformation. In a way this transformation can be understood as a hyperbolic rotation.
A quantity invariant under Lorentz transformations is known as a
Lorentz scalar.
Reference frames, coordinates and the Lorentz transformation Main article: Relativity of simultaneity Simultaneity Writing the Lorentz Transformation and its inverse in terms of coordinate differences we get


and
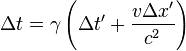
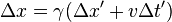
Suppose we have a clock at rest in the unprimed system S. Two consecutive ticks of this clock are then characterized by
Δx = 0. If we want to know the relation between the times between these ticks as measured in both systems, we can use the first equation and find:
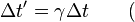
for events satisfying
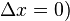
This shows that the time
Δt' between the two ticks as seen in the 'moving' frame S' is larger than the time
Δt between these ticks as measured in the rest frame of the clock. This phenomenon is called
time dilation.
Similarly, suppose we have a
measuring rod at rest in the unprimed system. In this system, the length of this rod is written as
Δx. If we want to find the length of this rod as measured in the 'moving' system S', we must make sure to measure the distances
x' to the end points of the rod simultaneously in the primed frame S'. In other words, the measurement is characterized by
Δt' = 0, which we can combine with the fourth equation to find the relation between the lengths
Δx and
Δx':

for events satisfying

This shows that the length
Δx' of the rod as measured in the 'moving' frame S' is shorter than the length
Δx in its own rest frame. This phenomenon is called
length contraction or
Lorentz contraction.
These effects are not merely appearances; they are explicitly related to our way of measuring
time intervals between events which occur at the same place in a given coordinate system (called "co-local" events). These time intervals will be
different in another coordinate system moving with respect to the first, unless the events are also simultaneous. Similarly, these effects also relate to our measured distances between separated but simultaneous events in a given coordinate system of choice. If these events are not co-local, but are separated by distance (space), they will
not occur at the same
spacial distance from each other when seen from another moving coordinate system.
See also the
twin paradox.
Time dilation and length contraction In diagram 2 the interval AB is 'time-like';
i.e., there is a frame of reference in which event A and event B occur at the same location in space, separated only by occurring at different times. If A precedes B in that frame, then A precedes B in all frames. It is hypothetically possible for matter (or information) to travel from A to B, so there can be a causal relationship (with A the cause and B the effect).
The interval AC in the diagram is 'space-like';
i.e., there is a frame of reference in which event A and event C occur simultaneously, separated only in space. However there are also frames in which A precedes C (as shown) and frames in which C precedes A. If it was possible for a cause-and-effect relationship to exist between events A and C, then paradoxes of causality would result. For example, if A was the cause, and C the effect, then there would be frames of reference in which the effect preceded the cause. Although this in itself won't give rise to a paradox, one can show that faster than light signals can be sent back into one's own past. A causal paradox can then be constructed by sending the signal if and only if no signal was received previously.
Therefore, one of the consequences of special relativity is that (assuming
causality is to be preserved), no information or material object can travel
faster than light. On the other hand, the logical situation is not as clear in the case of general relativity, so it is an open question whether or not there is some
fundamental principle that preserves causality (and therefore prevents motion faster than light) in general relativity.
Even without considerations of causality, there are other strong reasons why faster-than-light travel is forbidden by special relativity. For example, if a constant force is applied to an object for a limitless amount of time, then integrating
F=dp/dt gives a momentum that grows without bound, but this is simply because
p = mγv approaches infinity as
v approaches
c. To an observer who is not accelerating, it appears as though the object's inertia is increasing, so as to produce a smaller acceleration in response to the same force. This behavior is in fact observed in
particle accelerators.
See also the
Tachyonic Antitelephone.
Causality and prohibition of motion faster than light Main article: Velocity-addition formula Composition of velocities Main article: Mass in special relativity Mass, momentum, and energy Introductory physics courses and some older textbooks on special relativity sometimes define a
relativistic mass which increases as the velocity of a body increases. According to the geometric interpretation of special relativity, this is often deprecated and the term 'mass' is reserved to mean
invariant mass and is thus independent of the inertial frame, i.e.,
invariant.
Using the relativistic mass definition, the mass of an object may vary depending on the observer's inertial frame in the same way that other properties such as its length may do so. Defining such a quantity may sometimes be
useful in that doing so simplifies a calculation by restricting it to a specific frame. For example, consider a body with an invariant mass m moving at some velocity relative to an observer's reference system. That observer defines the
relativistic mass of that body as:

"Relativistic mass" should not be confused with the "longitudinal" and "transverse mass" definitions that were used around 1900 and that were based on an inconsistent application of the laws of Newton: those used
f=ma for a variable mass, while relativistic mass corresponds to Newton's dynamic mass in which
p=Mv and
f=dp/dt.
Note also that the body does
not actually become more massive in its
proper frame, since the relativistic mass is only different for an observer in a different frame. The
only mass that is frame independent is the invariant mass. When using the relativistic mass, the applicable reference frame should be specified if it isn't already obvious or implied. It also goes almost without saying that the increase in relativistic mass does not come from an increased number of atoms in the object. Instead, the relativistic mass of each atom and subatomic particle has increased.
Physics textbooks sometimes use the relativistic mass as it allows the students to utilize their knowledge of Newtonian physics to gain some intuitive grasp of relativity in their frame of choice (usually their own!). "Relativistic mass" is also consistent with the concepts "time dilation" and "length contraction".
Relativistic mass The classical definition of ordinary force f is given by
Newton's Second Law in its original form:

and this is valid in relativity.
Many modern textbooks rewrite Newton's Second Law as

This form is not valid in relativity or in other situations where the relativistic mass
M is varying.
This formula can be replaced in the relativistic case by

As seen from the equation, ordinary force and acceleration vectors are not necessarily parallel in relativity.
However the four-vector expression relating
four-force 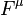
to
invariant mass m and
four-acceleration 
restores the same equation form
 Force
Force Main article: Minkowski space The geometry of space-time Here, we see how to write the equations of special relativity in a manifestly
Lorentz covariant form. The position of an event in spacetime is given by a
contravariant four vector whose components are:
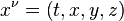
That is,
x = z. Superscripts are contravariant indices in this section rather than exponents except when they indicate a square. Subscripts are
covariant indices which also range from zero to three as with the spacetime gradient of a field φ:
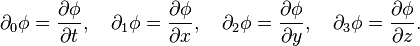 Physics in spacetime
Physics in spacetime Having recognised the four-dimensional nature of spacetime, we are driven to employ the Minkowski metric, η, given in components (valid in any
inertial reference frame) as:

Its reciprocal is:

Then we recognize that co-ordinate transformations between inertial reference frames are given by the
Lorentz transformation tensor Λ. For the special case of motion along the x-axis, we have:

which is simply the matrix of a boost (like a rotation) between the
x and
t coordinates. Where μ' indicates the row and ν indicates the column. Also, β and γ are defined as:

More generally, a transformation from one inertial frame (ignoring translations for simplicity) to another must satisfy:

where there is an implied summation of

and

from 0 to 3 on the right-hand side in accordance with the
Einstein summation convention. The
Poincaré group is the most general group of transformations which preserves the
Minkowski metric and this is the physical symmetry underlying special relativity.
All proper physical quantities are given by tensors. So to transform from one frame to another, we use the well known
tensor transformation law ![T^{left[i_1',i_2',...i_p'right>}_{left[j_1',j_2',...j_q'right]} = <br /> Lambda^{i_1'}{}_{i_1}Lambda^{i_2'}{}_{i_2}...Lambda^{i_p'}{}_{i_p}<br /> Lambda_{j_1'}{}^{j_1}Lambda_{j_2'}{}^{j_2}...Lambda_{j_q'}{}^{j_q}<br /> T^{left[i_1,i_2,...i_pright]}_{left[j_1,j_2,...j_qright]}](http://upload.wikimedia.org/math/8/5/9/85952e7f57d85491bacca39c7eb50a98.png)
Where

is the reciprocal matrix of
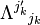
.
To see how this is useful, we transform the position of an event from an unprimed co-ordinate system
S to a primed system
S', we calculate

which is the Lorentz transformation given above. All tensors transform by the same rule.
The squared length of the differential of the position four-vector

constructed using
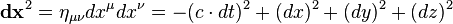
is an invariant. Being invariant means that it takes the same value in all inertial frames, because it is a scalar (0 rank tensor), and so no Λ appears in its trivial transformation. Notice that when the
line element 
is negative that

is the differential of
proper time, while when

is positive,
is differential of the
proper distance.
The primary value of expressing the equations of physics in a tensor form is that they are then manifestly invariant under the Poincaré group, so that we do not have to do a special and tedious calculation to check that fact. Also in constructing such equations we often find that equations previously thought to be unrelated are, in fact, closely connected being part of the same tensor equation.
Metric and transformations of coordinates Recognising other physical quantities as tensors also simplifies their transformation laws. First note that the
velocity four-vector U also has an invariant form:
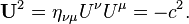
So all velocity four-vectors have a magnitude of
c. This is an expression of the fact that there is no such thing as being at coordinate rest in relativity: at the least, you are always moving forward through time. The
acceleration 4-vector is given by

. Given this, differentiating the above equation by
τ produces

So in relativity, the acceleration four-vector and the velocity 4-vector are orthogonal.
Velocity and acceleration in 4D The momentum and energy combine into a covariant 4-vector:

where
m is the
invariant mass.
The invariant magnitude of the
momentum 4-vector is:

We can work out what this invariant is by first arguing that, since it is a scalar, it doesn't matter which reference frame we calculate it, and then by transforming to a frame where the total momentum is zero.

We see that the rest energy is an independent invariant. A rest energy can be calculated even for particles and systems in motion, by translating to a frame in which momentum is zero.
The rest energy is related to the mass according to the celebrated equation discussed above:

Note that the mass of systems measured in their center of momentum frame (where total momentum is zero) is given by the total energy of the system in this frame. It may not be equal to the sum of individual system masses measured in other frames.
 Momentum in 4D
Momentum in 4D To use
Newton's third law of motion, both forces must be defined as the rate of change of momentum with respect to the same time coordinate. That is, it requires the 3D force defined above. Unfortunately, there is no tensor in 4D which contains the components of the 3D force vector among its components.
If a particle is not traveling at
c, one can transform the 3D force from the particle's co-moving reference frame into the observer's reference frame. This yields a 4-vector called the
four-force. It is the rate of change of the above energy momentum
four-vector with respect to proper time. The covariant version of the four-force is:

where

is the proper time.
In the rest frame of the object, the time component of the four force is zero unless the "
invariant mass" of the object is changing in which case it is the negative of that rate of change times
c. In general, though, the components of the four force are not equal to the components of the three-force, because the three force is defined by the rate of change of momentum with respect to coordinate time, i.e.

while the four force is defined by the rate of change of momentum with respect to proper time, i.e.

.
In a continuous medium, the 3D
density of force combines with the
density of power to form a covariant 4-vector. The spatial part is the result of dividing the force on a small cell (in 3-space) by the volume of that cell. The time component is the negative of the power transferred to that cell divided by the volume of the cell. This will be used below in the section on electromagnetism.
Force in 4D Theoretical investigation in classical electromagnetism led to the discovery of wave propagation. Equations generalizing the electromagnetic effects found that finite propagation-speed of the E and B fields required certain behaviors on charged particles. The general study of moving charges forms the
Liénard–Wiechert potential, which is a step towards special relativity.
The Lorentz transformation of the
electric field of a moving charge into a non-moving observer's reference frame results in the appearance of a mathematical term commonly called the
magnetic field. Conversely, the
magnetic field generated by a moving charge disappears and becomes a purely
electrostatic field in a comoving frame of reference.
Maxwell's equations are thus simply an empirical fit to special relativistic effects in a classical model of the Universe. As electric and magnetic fields are reference frame dependent and thus intertwined, one speaks of
electromagnetic fields. Special relativity provides the transformation rules for how an electromagnetic field in one inertial frame appears in another inertial frame.
Relativity and unifying electromagnetism Main article: Formulation of Maxwell's equations in special relativity Electromagnetism in 4D Main article: Status of special relativity Status Textbooks On the Electrodynamics of Moving Bodies, A. Einstein, Annalen der Physik, 17:891, June 30, 1905 (in English translation)
Wolf, Peter and Gerard, Petit. "Satellite test of Special Relativity using the Global Positioning System",
Physics Review A 56 (6), 4405-4409 (1997).
Will, Clifford M. "Clock synchronization and isotropy of the one-way speed of light",
Physics Review D 45, 403-411 (1992).
Rizzi G. et al, "Synchronization Gauges and the Principles of Special Relativity", Found. Phys. 34 (2005) 1835-1887
Alvager et al., "Test of the Second Postulate of Special Relativity in the GeV region",
Physics Letters 12, 260 (1964).
Olivier Darrigol (2004) "The Mystery of the Poincaré-Einstein Connection",
Isis 95 (4), 614 - 626.
Journal articles People:
Arthur Eddington |
Albert Einstein |
Hendrik Lorentz |
Hermann Minkowski |
Bernhard Riemann |
Henri Poincaré |
Alexander MacFarlane |
Harry Bateman |
Robert S. Shankland |
Walter Ritz Relativity:
Theory of relativity |
principle of relativity |
general relativity |
frame of reference |
inertial frame of reference |
Lorentz transformations |
Bondi k-calculus |
Einstein synchronisation |
Rietdijk-Putnam Argument Physics:
Newtonian Mechanics |
spacetime |
speed of light |
simultaneity |
physical cosmology |
Doppler effect |
relativistic Euler equations |
Aether drag hypothesis |
Lorentz ether theory |
Moving magnet and conductor problem Maths:
Minkowski space |
four-vector |
world line |
light cone |
Lorentz group |
Poincaré group |
geometry |
tensors |
split-complex number Philosophy:
actualism |
conventionalism |
formalism See also Original Works Wikibooks: Special Relativity Einstein Light An
award-winning, non-technical introduction (film clips and demonstrations) supported by dozens of pages of further explanations and animations, at levels with or without mathematics.
Einstein Online Introduction to relativity theory, from the Max Planck Institute for Gravitational Physics.
 with respect to S along the
with respect to S along the  -axis.
-axis. in system S and
in system S and 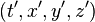 in S'. Then the Lorentz transformation specifies that these coordinates are related in the following way:
in S'. Then the Lorentz transformation specifies that these coordinates are related in the following way: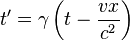

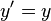

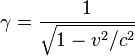 is called the Lorentz factor and
is called the Lorentz factor and  is the speed of light in a vacuum.
is the speed of light in a vacuum. and
and  coordinates are unaffected, but the
coordinates are unaffected, but the  and
and  axes are mixed up by the transformation. In a way this transformation can be understood as a hyperbolic rotation.
axes are mixed up by the transformation. In a way this transformation can be understood as a hyperbolic rotation.

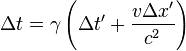
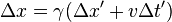
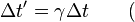 for events satisfying
for events satisfying 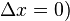
 for events satisfying
for events satisfying 




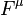 to
to  restores the same equation form
restores the same equation form
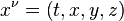
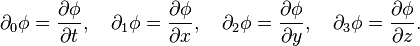





 and
and  from 0 to 3 on the right-hand side in accordance with the
from 0 to 3 on the right-hand side in accordance with the ![T^{left[i_1',i_2',...i_p'right>}_{left[j_1',j_2',...j_q'right]} = <br /> Lambda^{i_1'}{}_{i_1}Lambda^{i_2'}{}_{i_2}...Lambda^{i_p'}{}_{i_p}<br /> Lambda_{j_1'}{}^{j_1}Lambda_{j_2'}{}^{j_2}...Lambda_{j_q'}{}^{j_q}<br /> T^{left[i_1,i_2,...i_pright]}_{left[j_1,j_2,...j_qright]}](http://upload.wikimedia.org/math/8/5/9/85952e7f57d85491bacca39c7eb50a98.png) Where
Where  is the reciprocal matrix of
is the reciprocal matrix of 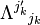 .
.
 constructed using
constructed using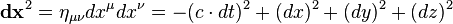
 is negative that
is negative that  is the differential of
is the differential of 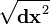 is differential of the
is differential of the 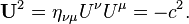
 . Given this, differentiating the above equation by τ produces
. Given this, differentiating the above equation by τ produces





 is the proper time.
is the proper time. while the four force is defined by the rate of change of momentum with respect to proper time, i.e.
while the four force is defined by the rate of change of momentum with respect to proper time, i.e.  .
.
No comments:
Post a Comment